Entre (parenthèses)
1 Problèmes (sans) complexes
"On résout les problèmes qu'on se pose et non les problèmes qui se posent." - Henri Poincaré
N°1 - Septembre 2018

ce.dsden11-mathematiques@ac-montpellier.fr
L’(Axe) des programmes
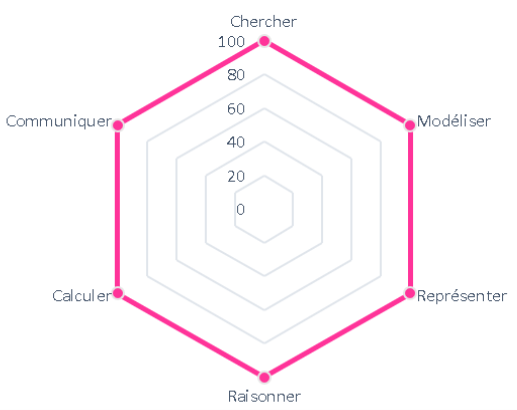
S’il y a bien un domaine qui touche à 100% l’ensemble des 6 compétences mathématiques, c’est sans nul doute la résolution de problèmes ! C’est d’ailleurs, peut-être, ce qui en fait sa complexité … Tout comme la production d’écrit, on est assez rapidement démuni devant l’ampleur de la tâche et, au fond, on ne sait pas vraiment par quel bout entrer … dans le problème.
La circulaire d’avril 2018 et les programmes de juillet 2018 confirment que la place de la résolution de problème est centrale : elle est à la fois la finalité et le moyen. Concrètement, un premier indicateur pourrait être pas de séance de maths sans au moins un problème à résoudre.
La circulaire insiste sur la nécessité d’un enseignement structuré et explicite, sur la construction et la collecte de situations de référence qui permettront la modélisation, la catégorisation et le transfert dans des problèmes inédits.
La proposition de mise en œuvre demande de ne pas négliger l’appropriation collective orale avant de laisser les élèves s’engager individuellement. Viendra ensuite le temps d’une éventuelle collaboration avec les pairs, avant de revenir collectivement (ou pas) sur un point particulier.
La programmation, progressive et exhaustive doit permettre aux élèves de rencontrer suffisamment de problèmes basiques, de problèmes complexes mais aussi de problèmes atypiques.
L’enseignant programme, encourage, relance, questionne, propose, guide, met en perspective, accompagne … grâce à sa fine observation des élèves.
L’(angle) des sciences cognitives
Les travaux de Jean Julo (enseignant chercheur en didactique des mathématiques) tendent à montrer que lorsqu’il est confronté à un problème, l’individu s’en construit une représentation mentale à l’issue de laquelle deux cas peuvent se présenter :
- le problème peut lui évoquer un autre problème, déjà résolu, c’est le système de la mémoire qui va être mobilisé.
- le problème n’est pas (re)connu et nécessite alors l’élaboration d’une nouvelle stratégie.
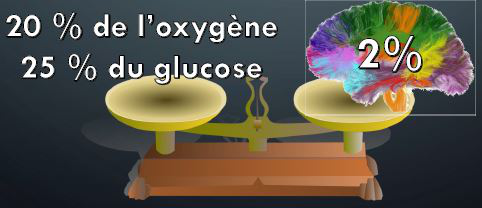
Or, le cerveau est un organe économe. Il représente 2% de la masse d’un individu mais consomme 20% des apports en oxygène et 25% du glucose.
Les fonctions exécutives : comme le système attentionnel, la flexibilité mentale, l’inhibition et la planification sont très énergivores. De plus, elles sont localisées à l’avant du cerveau, dans le cortex préfrontal d’une grande immaturité chez l’enfant. Ainsi, par défaut, le cerveau fonctionne systématiquement en mode « éco » et se repose sur ses automatismes plutôt que de mobiliser ses fonctions exécutives.
Ces données, conjuguées à ce que les sciences de l’éducation ont montré à propos du contrat didactique expliquent sans doute pourquoi, il est si difficile pour un élève d’inventer une stratégie, d’innover, de créer une réponse et pourquoi il est moins coûteux et plus rassurant pour lui de « bricoler » une réponse en se demandant ce que l’enseignant attend de lui, en s’appuyant sur du connu. Le capitaine en sait quelque chose ! Rolland Charnay parle de ces élèves qui cherchent dans leur tête, plutôt que de chercher avec leur tête !

Points de vigilance :
Ainsi, l’effort cognitif à fournir pour utiliser une soustraction dans un énoncé qui utilise le mot « plus » est considérable. Il demande à l’élève d’inhiber l’automatisme construit depuis son plus jeune âge : plus = addition. C’est pourquoi un travail sur les mots des énoncés est intéressant mais ne saurait se réduire à construire des catalogues de mots pour chacune des opérations, renforçant par là des automatismes qu’il faudra ensuite inhiber.

Par ailleurs, la (large) prédominance des problèmes basiques proposés aux élèves les conduit à systématiser : 1 problème = 2 données = 1 opération, les rendant incapables de traiter d’autres situations. Il est donc important de faire varier les problèmes proposés.
(Focale) : Modéliser
Modéliser c’est créer un «objet » qui, grâce à ses caractéristiques, à ses qualités, peut servir de référence à l'imitation ou à la reproduction.
Ce que l’on peut en retirer : à partir des schémas proposés et collectés par les élèves, certains invariants peuvent être remarqués et explicités. Les représentations personnelles vont ainsi évoluer vers une modélisation collective, négociée et comprise de tous, gage de son ancrage dans la mémoire individuelle et collective et de son exploitation dans d’autres situations.
Point de vigilance : Modéliser c’est « créer » le modèle. S’il est donné à l’élève avant que celui-ci ait pu agir mentalement sur sa conception, son élaboration, il deviendra un (n)ième outil/cadre/contrainte vide de sens responsable de bien des cheveux blancs de ce pauvre capitaine ! L’utilisation d’un « modèle mental » fait gagner du temps, mais avant, il en demande beaucoup pour son élaboration !
Les modèles en barres de la « méthode Singapour »
A Singapour, à l’école primaire, les élèves sont amenés à représenter leurs problèmes de maths sous une forme imagée, en barres.
Ces modèles permettent de visualiser les données connues et celles qu’ils faut trouver.

Rolland Charnay
« Un problème peut être défini comme une situation constituée d’informations qui peuvent être fournies sous des formes diverses (matériel, image, animation sur écran, énoncé oral ou écrit), avec un questionnement et dont la résolution nécessite une recherche, une investigation. En bref, la réponse ne peut pas être donnée immédiatement, mais nécessite un réel travail d’élaboration. »
Réussir en maths à l’école c’est possible !

Un (point) de classification …
Pour s’assurer que les élèves seront bien confrontés à un panel suffisamment représentatif de problèmes en voici une classification.
3 grandes catégories :
les problèmes « basiques » : l’énoncé fournit deux données, la troisième est à construire. Ces énoncés constituent la très grande majorité des problèmes proposés aux élèves.

On doit à Gérard Vergnaud une classification des problèmes basiques (voir ci-dessous).
les problèmes « complexes » : c’est une composition d’au moins deux problèmes basiques. Il faut construire des étapes de résolution.

les problèmes « atypiques » : ne peuvent pas se décomposer en problèmes basiques, ils nécessitent inventivité, raisonnement, tâtonnement …

Point de vigilance : L’intérêt de travailler une catégorisation particulière (type Vergnaud) avec les élèves pour améliorer leurs résultats n’a pas été montré (voir lien ci-dessous). Cependant, analyser, comparer, grouper les problèmes qu’ils ont résolus, selon une multitude de critères différents : leur complexité, le domaine sur lequel ils portent, la situation évoquée, les mots employés, leur modélisation … seront autant d’occasion d’explicitation, d’argumentation et participeront à la flexibilité mentale indispensable pour élaborer une stratégie de résolution.
http://centre-alain-savary.ens-lyon.fr/CAS/education-prioritaire/ressources/theme-1-perspectives-pedagogiques-et-educatives/travailler-sur-ce-qui-donnent-lieu-a-de-fortes-inegalites/mathematiques-en-education-prioritaire/categorisation-des-problemes-en-mathematiques-de-quoi-parle-t-onClassification des problèmes basiques – d’après Gérard Vergnaud
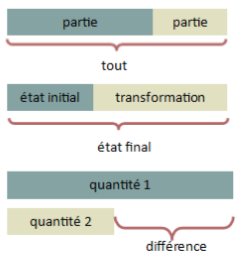
Structures additives (addition/soustraction)

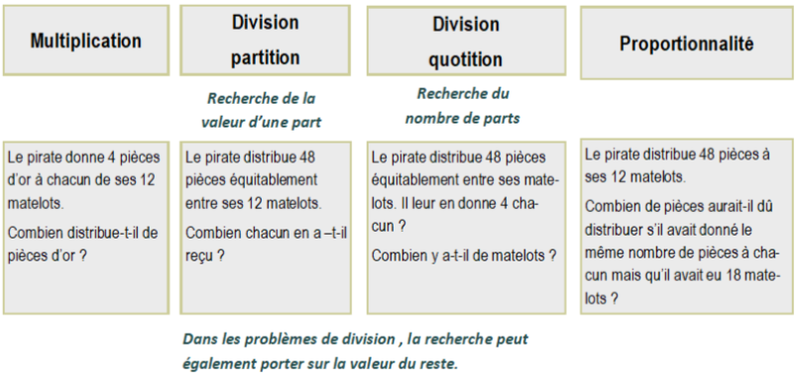
Structures multiplicatives
Pascale Toscani
Enseignante chercheuse en Neurosciences cognitives
« Ce n’est pas l’intelligence qui prédispose la compréhension … mais les apprentissages qui développent l’intelligence. Plus l’enfant traite d’informations différentes plus il développe la flexibilité de son intelligence et plus il peut intégrer de nouvelles connaissances. Au contraire, la simplification du milieu (en vue de ne pas surcharger, pour « aider ») aboutit à la « rigidité» du système cognitif et amoindrit sa capacité à apprendre. C’est donc une erreur pédagogique de donner moins d’informations à traiter à des enfants en difficulté. »